Antonio Salieri, an Italian classical composer, proposed to “check harmony by algebra.” But can we do the opposite and put algebra itself to a test? What if we attempt to put equations into pictures? This is certainly possible (and, no, we won’t be covering our calculations in rosebuds).
Today, let’s do something amazing to see how ordinary formal calculations can be replaced with pictures, or diagrams.
To get into the swing of things, let's start with simple equations. Before you know it, we'll get to the complex and unexpected ones. These equations are hard to believe. In fact, they are not easily proven even with the use of algebra. You may notice that all of our pictorial proofs are quite short. Rather than giving you lengthy text peppered throughout with tedious calculations, these proofs feature essentially just one phrase: “carefully examine the following diagram…”
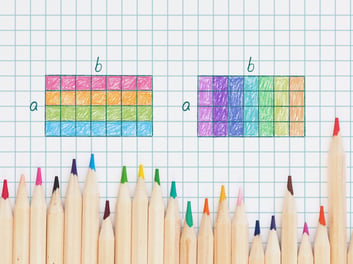
Let’s begin with the simplest example. This is something that we have learned early on in school – the commutative property of multiplication. We are so accustomed to this property that most us never question why, in fact, this is so.
a × b = b × a (that is, a + a + ... + a (b times) equals b + b + ... + b (a times))
Meanwhile, this property can be easily demonstrated using geometry, as shown.
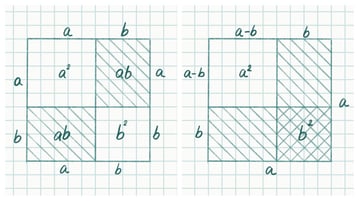Many of you will easily recognize which well-known equations the next set of pictures refer to! Here, a large square is divided into two smaller squares and two rectangles. The area of the large square equals to the combined areas of the four smaller shapes. If we calculate the areas of these shapes, then we will arrive at the special product equation: (a + b)2 = a2 + 2ab + b2.
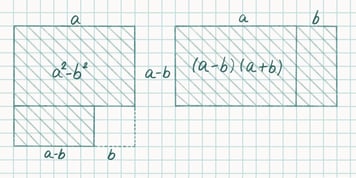In the next two diagrams, we see two more equations that should be very familiar to us from school. (a - b)2 = а2 - 2ab + b2 and
a2 - b2 = (a + b) × (a - b)
The last picture provides us with an easy way of finding an equation for the sum of the cubes.
Don’t you think that all of this is quite elegant? We have examined a mathematical equation using two completely different approaches and reached the same solution. Now we are ready for the more difficult, and hence more interesting, problems. It is time to draw some
more!
Problem 1.
Find the sum of the first n odd numbers.
Hint. Look carefully at the picture on the right. Diagrams 4 and 5 may also help with this problem.
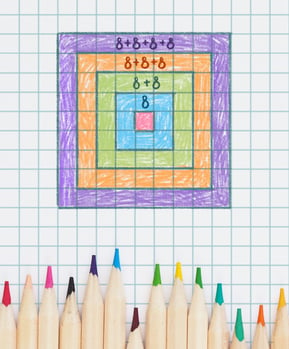
Problem 2.
How many more squares are there in the big frame than in the small one?
Problem 3.
Referring to diagram, explain the equalities below and continue the sequence.
1 × 1 = 1
3 × 3 = 1 + 8
5 × 5 = 1 + 8 + 2 × 8
7 × 7 = 1 + 8 + 2 × 8 + 3 × 8
9 × 9 = 1 + 8 + 2 × 8 + 3 × 8 + 4 × 8
11 × 11 = ?
13 × 13 = ?
15 × 15 = ?
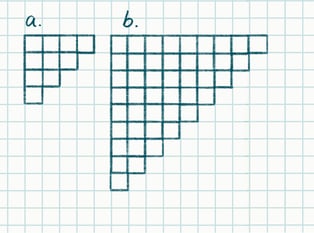Problem 4.
a) The diagram “a” contains a geometric shape. Create a rectangle out of two of these shapes. Is it possible to create a rectangle out of another two identical shapes, such as those in diagram “b”?
b) What is the sum of all numbers from 1 to n?
Problem 5.
Use geometry to explain the following equation:
1 + 2 + … + (n - 1) + n + (n - 1) + … + 2 + 1 = n2
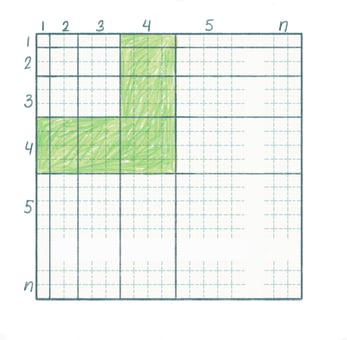Problem 6.
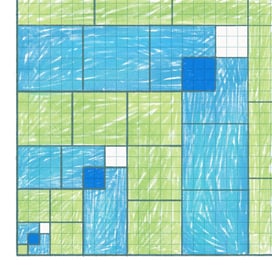
a) The picture shows the multiplication table of Pythagoras for numbers 1 to n. How many squares are there in the green corner? How many squares are there in the kth (‘thick’) corner?
Hint. Don’t count the green squares (only perhaps at the end to check your answer). Mentally divide this corner into two parts and use these parts to make a rectangle. What are the dimensions of this rectangle? Use problem 7 to help.
b) Find the sum 13 + 23 + … + n3 using the multiplication table of Pythagoras.
